“Sayı saymayı nasıl öğrendik? Sayılar nerden geldi? Neden bir diye adlandırdığımız rakam kare şeklinde gösterilmedi?” bunun gibi birçok soru gelebilir aklınıza… Bizler matematiği çok iyi yapabiliriz fakat geri plandaki temel tarihi es geçemeyiz. Sayıların dünyasına kendini kaptırmış birçok araştırmacı gün yüzüne çıkardığı esrarengiz belgelerle sayı şekillerinin temelinin nasıl oluşturulduğu sorusuna cevap vermemizi kolaylaştırdı. Özellikle Maya ve Babil uygarlıklarının sayıların gelişimi ile ilgili yaptığı çalışmalardan gün yüzüne çıkanlar bizlerin kafasında bazı şeylerin netleşmesini sağladı. Eski çağlarda insanlar sayma işlemini birebir eşleme yöntemi ile yapmaktaydı.
Özellikle arkeologların mağaralarda ve odun parçaları üzerinde buldukları çalışmalarda insanların herhangi bir şeyi saymak için her bir nesneyi karşılayacak bir çentik veya iz bırakırlardı. Özellikle eskiden insanlar hayvanlarını saymak için her bir hayvanı karşılayacak şekilde mağara duvarlarına kesikler atıp eksik olan hayvanlarını bu şekilde anlayabiliyorlardı. Çok çok eskiden ne kadar duvarlara ve odun parçalarına birebir eşleme yapılsa da Mısır medeniyeti matematiğin temellerini atmayı başarmıştır. Birebir eşlemeyi es geçip sayıların değerlerine karşılık bir nesne tanımlamışlardır. Hemen aşağıda da vereceğimiz üzere Mısır medeniyeti ile başlayan sayıya karşılık nesneler kuralı binlerce yıl süregelmiştir. Gördüğünüz gibi basamak ayrılırken üçlü bir sistem yerine ikili bir sistem tercih ediliyor. O dönem bu tarz bir sistemin kullanılması yılın kış ve yaz biçimde zamanın öğlen ve akşam biçiminde 2’ye ayrılması ile yakından ilişkili olduğunu görebiliriz. Hesaplama yaparken hata yapılmaması adına ikili bölüğü kullandıklarını söyleyebiliriz.
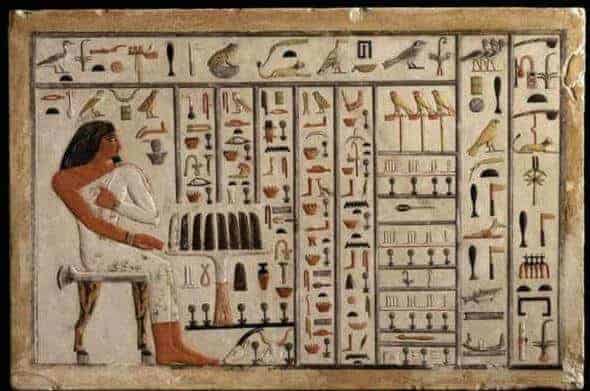
Özellikle Mısır matematiğine ilişkin bulgularımız “Papirüs” dediğimiz el yazmaları ile günümüze kadar ulaşmaktadır. En önemli ve en eski papirüsler üç döneme ayrılmaktadır. M.Ö. 1900 – 1800 yıllarına ait Kahun ve Berlin papirüsleri ile, M.Ö. 1700 ile 1600 yıllarına ait Hiksoslar Devrinden M.Ö. 1788-1580 kalma Rhind ve Moskova matematik papirüsleridir. İşte Mısır matematiğine dair tüm bildiklerimiz papirüsler, kil tabletler ve tahtanın üzerine yazılmış yazılardan ibarettir.
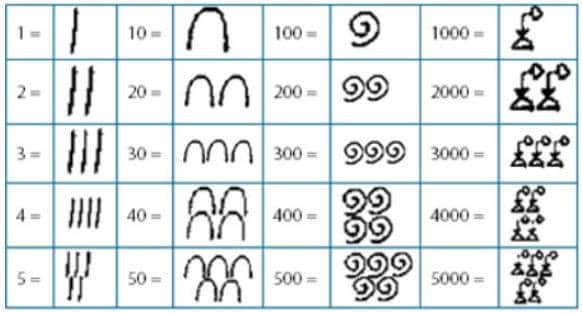
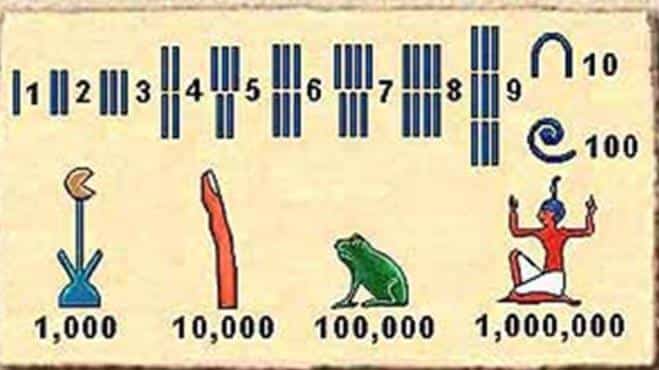
Mısır Medeniyetinde rakam ve sayılar bazı sembollerin yan yana gelmesiyle ortaya çıkıyordu. Hemen bir önceki sayfadaki Mısır sayı sistemine baktığınızda 1 için yukarıdan aşağıya çizilmiş bir çizgi, 10 için bir at nalı, 100 için çengele benzeyen bir nesneler kullanılmış, herhangi bir sayıyı yazmak için ise yine günümüzdeki gibi sağdan sola doğru bir biçim kullanılmıştır. Ama bu sayı sisteminde bir sorun vardı. 1 milyondan daha fazla olan sayılar ifade edilemiyor bu sayılar için “Şaşkın adam” sembolü kullanılıyordu. Yani 1 milyon ile 15 milyon sayılarını anlamak imkansız bir durum oluyordu. Mısır Medeniyetine ait bu sayı sistemindeki diğer bir karmaşa ise 123 sayısını yazdığınızda 231 ve 321 sayılarına da denk gelen aynı yazım biçimi olduğundan sayıyı yazan kimsenin hangi rakamı gösterdiği imkansız oluyordu. Çünkü yukarıdaki bu üç sayının Mısır sayı sistemine göre yazımı aynıydı. Tabloyu incelediğinizde 6 sayısını ifade etmek için 6 tane çubuk kullanmanız gerekiyor. 95 sayısını ifade edebilmeniz için toplam 18 999 sayısını ifade etmek için ise 27 ayrı şekil kullanılması gerekmektedir. Sizin de tahmin edeceğiniz üzere 13493 gibi bir sayıyı yazmak çok güç.
Bu sayı sisteminde 10’luk sistem mevcuttu. Herhangi bir grupta bulunan 10 nesne başka bir sembolle gösterilmekteydi. Mesela 10 sayısına baktığınızda yüksük kemiği ile gösterilmesi gibiydi. Yani 9 tane dik çizgiden sonra ( ki bu 9 rakamını gösteriyordu ) attığınız bir çizgi 10’luk sisteme geçeceğinden dolayı farklı bir sembole tekabül edecektir. Bu ise sayı sistemindeki karışıklığı azaltmıştır.
Matematiğin yazılı döneminin ilk dönemi olan Mısır ve Mezopotamya dönemi birçok matematiksel bilginin tavan yaptığı dönem olduğu biliniyor. İşte günümüze gelen ve o çağlarda Mısırda yapılan matematik hakkında bilgi almamızı sağlayan iki adet papirüs ünlü İskoç Antikacı A. Rhind tarafından gün yüzüne ulaştırılmıştır. İşte bahsettiğimiz tüm bu sayı sistemlerinde bu papirüslerin detaylı okunması ile bilgi aldık. İlk papirüs olan Ahmes veya diğer adıyla bilinen Rhind papirüsü Mısır’ın en önemli matematikçisi olan Ahmes tarafından kaleme alınmıştır. Ahmes, Mısır hükümetinin görevlendirdiği bölgedeki arazileri ölçen bir geometriciydi. Geometri bilgisi iyi olduğu kadar matematiksel aritmetik yeteneği de üst düzeydeydi. Zaten kendi adıyla anılan papirüs kağıdında da pi sayısıyla ilgili yaptığı çalışmalar bu söyleneni desteklemekteydi. Yaklaşık 6 metre uzunluğunda ve 35 cm genişliğinde olan bu papirüsün yazılma amacı sadece insanlara matematik öğretmektir. Çok zor olmayan henüz ortaokul matematik bilgisine sahip bir insanın bile çözebileceği bu problemler matematik günlük hayatı kolaylaştırmak içindir ifadesi için yazılmıştır. İçinde faiz problemleri, temel kesir problemleri (mirasları paylaştırmak adına) ve geometrik şekillerin çevre ve alan kuralları basit düzeyde anlatılmıştır. Ahmes papirüsün hemen sağ alt tarafına da pi sayısının yaklaşık değerini hesaplama gayretine girmiştir. Rhind papirüsünü bulan Antikacı H. Rhind adıyla anılan bu papirüs İngiltere müzesinde sergilenmektedir. M.Ö. 1900’lü yılların matematiğini anlatan bu papirüs ile birlikte yeni bir papirüs olan Moscow papirüsünün bulunmasıyla insanoğlunun matematiğe olan bakış açısı değişti. Burada sorusu olan yok sanırım. Asıl ilginç olan şeylere henüz başlamış değiliz.
Hani Moscow papirüsü dedik ya! İşte bu papirüs M.Ö 1600’lü yıllarda yazıldığı anlaşılan biraz daha zor bilgiler içeren ikinci en önemli matematik belgesidir. Bu papirüs belgesinde de toplam 25 soru bulunmaktadır. Bu sorular hemen hemen Ahmes papirüsündeki gibi zorluk düzeyine sahip olsa da 2 soru çok zor ve şaşırtıcıdır. Çünkü dönemin matematiksel bilgi düzeyi göz önüne alındığında bu soruyu sormanın imkansız olduğu görülmektedir. İlk soru bir düzlem ile kesilen piramidin hacminin nasıl bulunacağı üzerineydi. Piramit ile ilgili soruların sorulması o dönemlerde yapılan piramit şeklindeki anıt mezarların biçimsel detaylarını oluşturmak amacıyla sorulmuş olma ihtimali çok yüksek gözükmektedir. Diğer soru ise ilkinden biraz daha zor gibi gözükmektedir. Herhangi bir doğrunun bir küreyi kesmesi ile oluşan bölünmüş küre parçasının hacminin nasıl hesaplanacağı üzerineydi. Moscow papirüsünü incelediğimizde bu iki sorunun da çözümünün doğru bir biçimde çözüldüğünü görebiliriz.
Bu papirüsler matematikçiler tarafından detaylı bir şekilde incelendiğinde Mısır medeniyetinin matematiğinin zirvede olduğunu görmüşlerdir. Sürekli yuvarlak nesneler çizip bunların çevresi ve çapı arasındaki bağıntıyı takıntı haline getiren Mısırlılar pi sayısının varlığını ilk bulan medeniyet olarak tarihe geçmişlerdir. Mezopotamya’da yapılan matematik Mısır matematiğine göre daha anlaşılır ve daha çok yazılı kaynakla o dönemin şartlarını anlamaya yetmiştir. Mezopotamya’da kullanılan yazılı belgeler papirüs yerine “kil tablet” diye adlandırdığımız balçık ve çamurdan yapılmış yüksek sıcaklıkta pişirilen ve uzun süre korumaya bırakılan 30 cm genişliğinde yazılı belgeler mevcuttu. İstanbul başta olmak üzere Berlin, Moskova, İngiltere, Yale gibi birçok kentin müzesinde sergilenmektedir. Çıkarılan 2000’nin üzerindeki kil tabletlerden sadece 500 kadarında matematiksel bilgiye ulaştığımızı söylemekte fayda var. Bu bölgelerdeki matematik ( Mezopotamya matematiği ) Mısır matematiğinden daha ileri bir seviyede olduğu net gözlemlenmektedir. Söylemiştik ya Mısır matematiği ortaokul matematiği düzeyindedir diye Mezopotamya matematiği ise lise matematiği düzeyindedir. Onlar Mısır matematiğini çok iyi bildikleri gibi ek olarak bazı polinomların çözümlerini, köklerinin bulunmasını ve yeni bir sistemin nasıl yazılacağını biliyorlardı. Ek olarak “Pisagor! Teoremi” diye adlandırılan dik üçgenin kenarları arasındaki bağıntıyı veren formülü de çok iyi bir şekilde kullanabilmekteydiler. Zaten derin araştırmalar yaptığımız zaman Pisagor’un bir dolandırıcı olduğunu (bu noktada birçok matematikçi Pisagor’un kendinden yıllar önce bulunan birçok teoremi kendi adını kullanarak yayınlandıklarını söylemektedir.) görmekteyiz. Mısırlılar pi sayısının varlığını bulmalarına rağmen yukarıda da bahsettiğimiz üzere ellerine aldıkları tüm çemberlerin çevrelerinin çapları ile ilişkili olduklarını görmüşlerdir. Ama bu sayının kaç olduğunu bir türlü hesaplayamamışlardır.
Mezopotamya’da ise pi sayısı için karesi 10 olan sayı tanımı yapılmış ve daha sonra bir sayının karesinin nasıl alınacağı öğrenilince 3.15 gibi profesyonel bir sonuç bulmuşlardır. Mısır ve Mezopotamya matematiğinde formül, teorem ve ispat gibi pür matematik terimleri yoktu. Matematiği kullanmalarının sebebi ise hayatı kolaylaştırmaya yönelikti. Geometrik çizimler hariç (bunlara ispat diyen matematikçi kesimi de mevcuttur.) sayısal anlamda bir ispata gerek duymamışlardır. Günlük hayatın bir parçası, bir gereksinimi olarak doğan matematik miras, inşaat, dini ve milli günleri belirlemede, deniz yolculuklarında yön tayini, tarıma uygun bölgelerin şekillerinin çıkarılması gibi birçok ihtiyacın sonucunda doğmuştur. Zaten “Matematik nasıl ortaya çıkmıştır?” şeklinde bir soru sorarsak bunun cevaplarından ilki hemen yukarıda saydığımız nedenlerden dolayıdır. Bu dönemi bitiren Pers imparatorluğunun istilası ile bir matematik dönemi kapanmış matematiğe dair çalışmalar uzun süre sessizliğe gömülmüştür.